Dictionaries are made from Tries

cs50 pset 5 was all about data retrieval and memory management, so the challenge was to implement a searchable dictionary that could be used to quickly implement a spell checker on entire books (like the Bible or a Tolstoy novel).

Whenever working with data, you're always making tradeoffs between speed and resources. What might be fastest will require more memory, or the solution that requires minimal resources might take twice as long to complete the task.

Since speed was of the essence for a spell checker, I chose to err on the side of speed, so I went down the route of tries. It promised the quickest lookup of each word in a book, but would require more memory.

To give you an idea of what I was building, check out the following diagram:

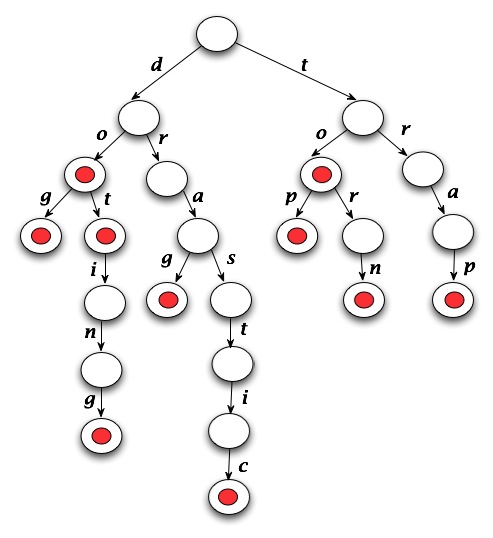
Basically the idea is that each node contains an array of pointers, one for each possible letter. Each word progresses down the tree, letter by letter, and a red dot signifies the end of a word. So, if you're looking for the word "top", you can progress down the nodes and find a red dot.

But if you were looking for "toad", you would discover after your third traversal of the tree that it was not in the dictionary because there is no "a" node under t->o.

Nodes

So the first step is defining each node as a structure:

// Node Definition
typedef struct node
{
    bool is_word;
    struct node* children[27];
}
node;

Each node contains a Boolean value of whether or not this node is the completion of a word, and an array of 27 pointers to other nodes. These nodes represent the possible 26 English characters plus an apostrophe.

To do this we just do a quick lookup function to find the position of each letter in the array. If it's an apostrophe, we return the last position, otherwise we get the position based on how many chars it is from lowercase 'a'.

/**
 * Returns index of letter within trie array
 */
int getIndex(const char c)
{
    if (c == '\'') 
    {
        return 26;    
    }
    else 
    {
        return tolower(c) % 'a';
    }
}

Loading Words into the Dictionary

Now we take a dictionary file, formatted where each word is on a separate line, and load it into memory.

The dictionary would look like:

apple
banana
carrot
...

Obviously with way more words, and then we would load them like so:

/**
 * Loads dictionary into memory.  Returns true if successful else false.
 */
bool load(const char* dictionary)
{
    // Create space for root
    root = malloc(sizeof(node));
    
    // Initialize number of nodes
    total_nodes = 0;
    
    // Read dictionary
    FILE* fp = fopen(dictionary, "r");
    if (fp == NULL)
    {
        printf("Could not open %s.\n", dictionary);
        unload();
        return false;
    }
    
    // Set cursor to root
    node* cursor = root;
    
    // Read each character in dictionary
    for (int c = fgetc(fp); c != EOF; c = fgetc(fp))
    {
        // Check if newline
        if (c == '\n') 
        {
            // mark as word
            cursor->is_word = true;
            
            // Increment number of nodes
            total_nodes++;
            
            // reset cursor to root to traverse trie again
            cursor = root;
        }
        else 
        {
            // Find the index of the letter
            int index = getIndex(c);
            
            // Check if node exists for letter
            if (cursor->children[index] == NULL) 
            {
                // Create new node
                cursor->children[index] = malloc(sizeof(node));
            }

            // Move to next node
            cursor = cursor->children[index];
        }
    }
    
    // Close dictionary
    fclose(fp);
    
    return true;
}

Note that each time we hit a newline, we mark the Boolean of the current node as true. Also note that the program is reserving space for a new node at each new letter it encounters, otherwise it keeps traversing the tree.

Check if word is in dictionary

Now that the dictionary is loaded into memory, we can begin to check words given to the program to see if they match or not.

/**
 * Returns true if word is in dictionary else false.
 */
bool check(const char* word)
{
    // Set cursor to root
    node* cursor = root;
    
    // for each letter in input word
    for (int i = 0; word[i] != '\0'; i++) 
    {
        // Find the index of the letter
        int index = getIndex(word[i]);
        
        // got to corresponding element in children
        if (cursor->children[index] == NULL) 
        {
            // if NULL word is mispelled
            return false;
        }
        
        // if not NULL, move to next letter
        cursor = cursor->children[index];
    }
    
    // once at end of input word, check if is_word is true
    return cursor->is_word;
}

The cursor moves down the tree, and returns whether or not the word was found. If at any point it hit a null pointer, or the Boolean of the node was set to false, then we know it's not in the dictionary.

Freeing memory

Once the spell check progress is complete, we need to unload the dictionary and free up all of that memory we used!

/**
 * Check node children to see if they can be freed
 */
bool free_nodes(node* ptr)
{
    // Go through node's children
    for (int i = 0; i < 27; i++)
    {
        // If child is pointer, recursively check that one as well
        if (ptr->children[i] != NULL) 
        {
            free_nodes(ptr->children[i]);
        }
    }
    
    // If all chilren are null, free node
    free(ptr);
    
    return true;
}

It's a recursive function that makes sure all of the children nodes are freed before freeing a parent node, otherwise we lose track of the child nodes completely! Since I went down the route of using more memory for the sake of speed, this is especially important.

Overall this method worked surprisingly well. I was never able to match the speed of the staff's solution, but I was still able to check the entire King James Bible in around a second, which is pretty cool!

As always, for the full exercise, check out my Github Repo.